Birthday paradox
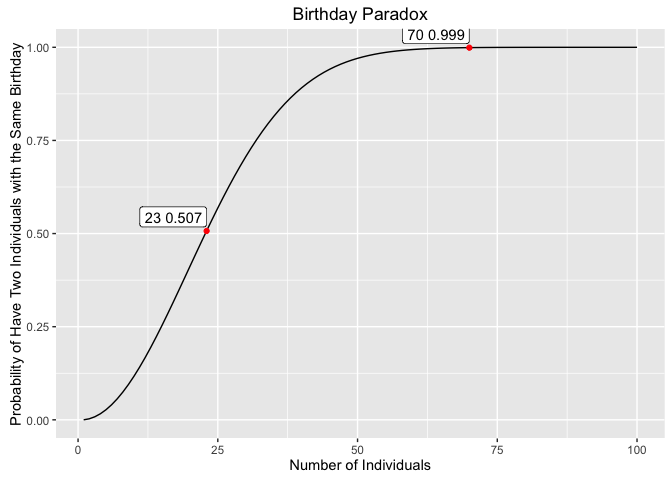
In a set of n randomly chosen people, some pair of them will have the same birthday. By the pigeonhole principle, the probability reaches 100% when the number of people reaches 367. However, 99.9% probability is reached with just 70 people, and 50% probability with 23 people based on the assumption that each day of the year is equally probable for a birthday.
Calculating the probability
x <- rep(NA, 100)
y <- rep(NA, 100)
p <- rep(NA, 100)
x[1]=1
y[1]=1
p[1]=0
for(i in 2:100)
{
x[i]=i
y[i]=y[i-1]*(365-i+1)/365
p[i]=1-y[i]
}
dat = data.frame(numOfIndiv=x, prob=p)
dat2370 = dat[dat$numOfIndiv==23 | dat$numOfIndiv==70,]
dat2370$prob <- round(dat2370$prob, digits=3)
Plot the probability
library(ggplot2)
ggplot(dat, aes(x=numOfIndiv, y=prob)) +
geom_line() +
xlab("Number of Individuals") +
ylab("Probability of Have Two Individuals with the Same Birthday") +
ggtitle("Birthday Paradox") +
geom_point(data=dat2370,aes(x=numOfIndiv, y=prob), colour = "red") +
geom_label(data=dat2370,
aes(x=numOfIndiv, y=prob,
label=paste(numOfIndiv,prob,sep=" ")),
hjust = 1, vjust = -0.2)