“Odds ratios are not well understood as a measure of effect size, and conversion to relative risks by a simple calculation would improve understanding of findings”
relativeRisk = oddsRatio / (1 - baselineRisk + oddsRatio * baselineRisk)
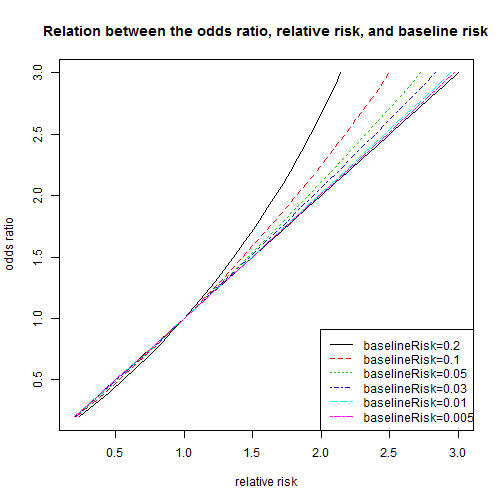
The odds ratio is always further away from 1 than the relative risk, but they are more similar when the baseline risk is small.
Definitions of odds and risks
<TABLE border=1>
</TABLE>
Outcome present for treatment: a
Outcome present for control: b
Outcome absent for treatment: c
Outcome absent for control: d
Total for treatment: a+c
Total for control: b+d
Total for present: a+b
Total for absent: c+d
Odds can range from 0 to infinity but are always positive.
Odds of the outcome in the treatment group: a/c
Odds of the outcome in the control group: b/d
Odds ratio
Odds ratio for the outcome comparing treatment with control: (a/c)/(b/d)=(a×d)/(b×c)
Risks can range from 0 to 1.
Risk of the outcome in the treatment group: a/(a+c)
Risk of the outcome in the control group: b/(b+d)
Relative risk
Relative risk comparing treatment with control: (a/(a+c))/(b/(b+d))=(a×(b+d))/(b×(a+c))
- For both the odds ratio and relative risk, 1 represents no difference between the groups
- The risk (and the odds) does not have to refer to an undesirable outcome
- risk = odds/(1+odds)
“Most published research providing an odds ratio as a measure of effect size should also provide sufficient information for the baseline risk, and hence the relative risk, to be calculated. If numbers in each group are given, the crude relative risk can be calculated directly.” – BMJ 2014;348:f7450 doi: 10.1136/bmj.f7450
Reference
- Converting an odds ratio to a range of plausible relative risks for better communication of research findings. BMJ 2014;348:f7450 doi: 10.1136/bmj.f7450